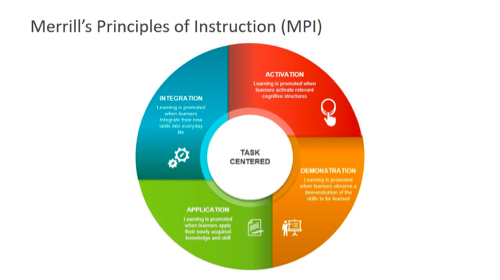
A lesson that I believe could be built using Merrill’s 5 design principles is teaching younger students how to successfully solve a long-division math equation. The first principle is “Learners are engaged in solving real-world problems” (Merrill, 2002). Within this principle, learning is promoted when the learners are shown an example of the task that they will be able to complete by the end of the module, and with long division, the teacher would be able to show an example and the process needed to complete the question before engaging in the module. The students existing knowledge will be activated through learning the process of long-division as they will need to recall their acquired math skills regarding division, multiplication, addition, and subtraction. Already knowing these skills will allow them to build on these skills through long-division. The third principle states that “new knowledge is demonstrated to the learner” (Merrill, 2002). This can be achieved through the use of examples, demonstrations of the procedures, visualization processes, and modelling of behaviours (Merrill, 2002). All these methods can be used and implemented when teaching long division, which also gives the advantage of tailoring to many different ways of learning which will benefit the students. The knowledge can then be applied by the learner as they attempt and learn how to solve these mathematical equations, using all the skills they have built up to this point. With the final principle being “new knowledge is integrated into the learner’s world” the students will then be able to take this new skill and apply it to the rest of their schooling (Merrill, 2002). It provides the ability to continue practicing their basic skills of division, multiplication, addition, and subtraction which will be needed for the rest of their lives.
References:
Merrill, M. D. (2002). First Principles of Instruction. ETR&D, 50, 3. pp. 43-59.
Hi Megan,
Great job on your blog post! I was impressed with how well you were able to apply Merrill’s 5 design principles to teaching long-division to younger students. Your post was very clear and well-organized, and I appreciated how you provided specific examples of how each principle could be applied in the context of math education. I particularly liked how you highlighted the importance of engaging students in real-world problems to help motivate them and give them a sense of what they are working towards.
Hi Megan! I thought that the application of Merrill’s design principles to teaching mathematics was a great example of these principles can be applied to learning. I feel as though STEM topics can be harder to break away from the heavily guided style that’s more normal nowadays, but what you explained really makes sense.
It helped me understand the principles myself too, so I actually think in turn you have made a good way to teach somebody about Merrill’s 5 instructional design principles!
Hi Megan,
Thank you for your insightful post. It is true that interactive learning can help students retain information and generate an inclusive hands-on learning experience that can help students stay interested in the topic at hand. More specifically, teaching young students how to solve long-division math equations can be difficult; however, by employing Merrill’s five design principles, instructors can create engaging lessons that help students understand principles and apply what they have learned in their daily lives. As a result, I agree that by applying Merrill’s principles, leaners can obtain valuable competencies and skills that they can apply in their daily environments, making the lesson valuable for both educators and students.